Quirks UVM architecure overview

Top

Introduction

The Quirks project goal is a creation of an universal virtual machine which will make possible an object migration in boundaries of some heterogenous distributed system. Some attempt of classification of distributed systems is below. Requirements to our virtual machine follow after that.

1 Some patterns of the approach we are interesting in.

Distributed systems can be conditionally divided to 4 categories, each next inherits all of features of a previous.

1. The set of collaborating components which are running on different computers and communicate by well defined protocol.
2. The set of components whose collaboration is based on a system of common types which allow data migration. The simplest way is to use one language (as we have with Ada Annex E approach). Another example - use some common type definition mechanism which will be mapped on a set of languages (IDL approach).
3. The set of components with an object migration mechanism. In this case not only data can migrate but behavior as well and we need some common virtual machine.
4. The set of components whose collaboration wasn’t planed by introducing common declarations. In this case we could talk about dynamic typing when a type description is transmitted together with a data. The type description will allow working with the data on another side.

2 The requirements to the Quirks UVM design.

1. JIT compiler should produce a fast native code. fast means it should be no less effective than a code produced by compilers (for example, C compiler).
2. We need a possibility of UVM code interpretation which should be no less effective compare to another VM (we choose a Java VM to compare with).
3. The possibility of targeting from wide range of languages (C/C++, Ada-95, Mercury, Lisp as a minimum).
4. It must provide a data security when we call functions from untrusted libraries, i.e. all possible changes in a data must be defined by a procedure call specification.
5. The set of supported data types should not be constrained by some finite set (which is found by intersect dataset of modern universal CPUs) but should be extendable, allow support a date of any capacity, structure (for example bit fields, images etc.) for most effective use of features of any future processors.
6. The set of operations should be extendable (see the previous requirement).
7. The working with a data would be descriptor-based. See Classification.

3 The Quirks UVM architecture.

3.1 Descriptors and structures

A descriptor is a remedy for dynamic type description. A descriptor contains full set of information needed for working with data ever in the case the data were come from unknown sender and this sender knows nothing about us.

In general case a descriptor contains an information of 4 layers:

1. A logical data organization.
2. An read/write modes.
3. An information about referenced elements.
4. A memory offset for different elements.

We say that layers 1-2 belong to a type, 3-4 to layout.

A logical data organization is the first thing we need to know. Whether the type is an enumerate, integer, float, which format it uses, is the data a structure, array, what this structure (array) includes as elements?

For our goals a logical organization can be presented as a tree. In that tree leafs equals to atomic types and nodes to complex types¹.

These are the Quirks atomic types:

• bit1
• int8
• int16
• int32
• int64
• uint8
• uint16
• uint32
• uint64

... (floating types should be added).

The types int8 int16 int32 int64 represent signed integer types and uint8 uint16 uint32 uint64 - unsigned integers. The bit1 is the type which represents 1 bit.

These are the Quirks complex types:

• stu - represents a structure (for example ‘<int8 int16 stu>’ - a structure from 2 elements).
• arr - the array (‘<int8 arr 10>’ - 10 bytes).
• dis - the discriminated type.

By using this set of types we can describe more complex types, for example:

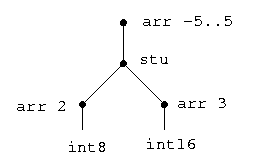
<<<int8 arr 2> <int16 arr 3> stu> arr -5..5>

and the descriptor tree will look in the following way:

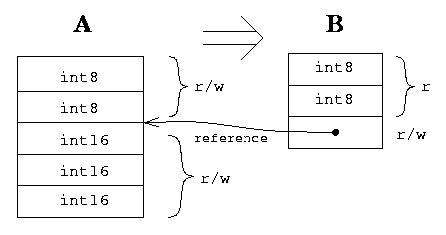
Another kind of information which can be found in any descriptor is the data about access modes to elements (an element is the data correspond to any node or leaf of a descriptor if you see on it as on a tree). There are two basic variants - read (r) and write (w). From those basic variants we can produce 4 access mode: no access, r, w, r/w. I.e., access mode is a set of two possible elements - read and write. We can say that the one mode is wider than another if its set is a strict inclusion of set of another mode. There is a rule about modes in a descriptor: the mode of any node is a sum of sets of all sub elements.

Any descriptor only describes a type. The described data is organized as a structure (the term is slightly overloaded). In the easiest case a structure is a continuous memory block. For example, let consider the descriptor:

<<uint8 arr 2> <uint16 arr 3> stu>

The corresponding structure can looks like the following:

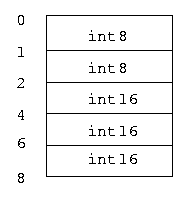
Really, the descriptor contains not only information about the data organization but memory layout also. The same data may be represented, for example, as follows:

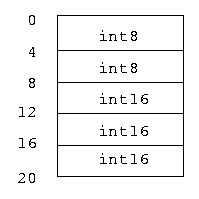
(the alignment on a 32-bit boundary)

or as follows:

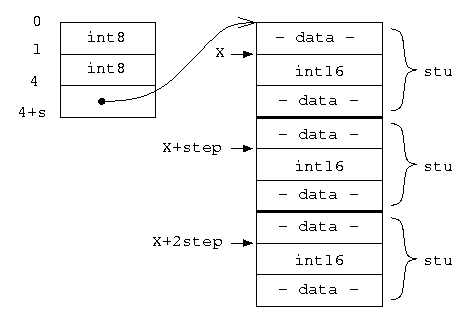
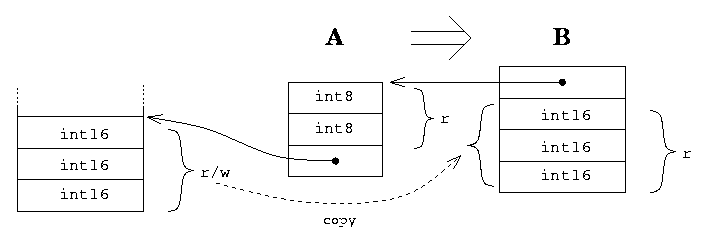
(the A structure contains a reference to the B structure. Thus, the B structure is an element of the A structure. B, generally speaking, can has some different organization, in our case ‘<<~TYPE1 int16 ~TYPE2 stu> arr X>’. It is deal of the B descriptor to virtually represent B as an array ‘<int16 arr>’ (it can be done very easy because all ‘int16’ elements are situated with the same step in the memory).

Descriptors are incompatible if they describe different logical data organization.

Descriptors are memcpy-compatible if they are compatible on the all 4 layers. In this case data from one structure to another can be transmitted by simple copying of the memory block (‘memcpy’).

Accordingly, descriptors can be partially compatible (in this case we could talk about 1, 2, 3-level compatibility).

We define access operation as a reading/writing operation of a logical structure element (as well as whole structure as an element). The access performs with order which is a sequential specification of logical element selection.

... (some examples of ordering should be added).

3.2 Mapping

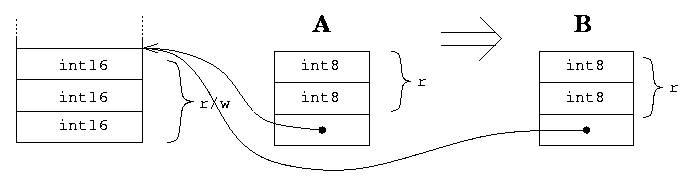
The mapping of the structure A onto the structure B is the operation of B structure memory change which results such way that all access operation to the B and A structures will be equivalent.

Two structures are compatible for mapping if

1. they are level 1 compatible;
2. the modes of all structure A elements are wider than the corresponding modes of the structure B (see wider).

3.2.1 Mapping examples

3.2.2 The mapping mechanism

We always can map with a reference. The mapping with a copy can be performed only in the case when the destination element has a r mode (under the condition of no changing A ‘read B’ will be equivalent to ‘read A’.

3.3 Arithmetic modules and a mapping

Arithmetic expression is a kind of a mapping. Let’s see on the following expression:

x = 3 * a + 4 * b

The mapping can be represented with the following scheme

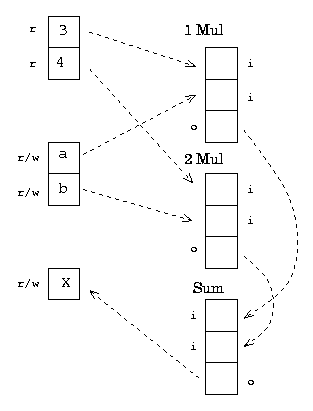
The ‘1Mul’, ‘2Mul’ and ‘Sum’ are special - they represents concrete ALUs (in this case ‘1Mul’ and ‘2Mul’ are multipliers and ‘Sum’ is a adder). An ALU module guarantees that its elements there are in some relation one with others, for example

Sum[0] + Sum[1] = Sum[2]
Mul[0] * Mul[1] = Mul[2]

The properties are defined by the module type; the roles of elements are positional bounded in the each type (for example, ‘Sum[0]’, ‘Sum[1]’ always are components and ‘Sum[2]’ always is the sum).

ALU modules can be more complex. The Quirks UVM has a standard module ‘Iul’ (or Integer multiplier) that has the following structure:

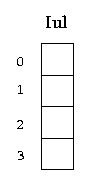
For its elements the following relation is true:

Iul[0] * Iul[1] + Iul[2] = Iul[3]

(i.e., adder and multiplier in the one module).

A function of each module is turning the elements in accordance with the module function. Such turning is based on modes of the elements (in this case, better say about input/output modes than about access modes). For example, a adder in the mode ‘iio’ sums the elements 0 and 1 but in the mode ioi subtracts the element 2 from element 0 and the element 1 is a result. The ‘Iul’ module in the mode ‘iooi’ performs an integer division with remainder and so on. (It should be pointed here that ‘i/o’ mode is illegal for an ALU element).

Thus, a semantic of an ALU module is not restricted by a procedural semantic but it allows to represent arithmetic expression in logic programming languages (Mercury, Prolog).

For complex expressions the conception of arithmetic mapping is used. In this context an expression is equivalent of a module which consists of some number of a basic modules. For example, an expression from the last picture can be represented as follows:

[4] = [0] * [2] + [1] * [3]

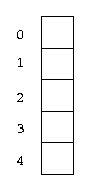
As for any module, the expression functionality is determined by modes of elements. In this case all the following modes make sense:

iiiio    (look for X)
iiioi    (look for b)
iioii    (look for a b coefficient)
ioiii    (look for a)
oiiii    (look for an a coefficient)

The modes of an whole expression determine in order the modes of its basic arithmetic modules.

A mapping of memory structures elements on arithmetic units (as well as arithmetic units on another arithmetic units) seams like a mapping of memory elements as was described above. The arithmetic mapping is an extension of the mapping notion.

A mapping is relation between elements of two structures. The mapping functioning is turning elements in an accordance based on input/output modes of each element.

A mapping without arithmetic units is names 0-mapping. All mappings besides 0 use one or more basic arithmetic units.

3.4 Generic features

In the section about arithmetic modules was nothing about types. It is not accidentally: the module defines an operation. The data type defines value and operation set (the data typing view). Here we say about operation typing and in such approach the operation type defines a value semantic for which the operation has a sense. Any arithmetic module defines a semantic of operations. The UVM can work such way that real arithmetic module selection (statically data typed) will be determined in runtime. Thus, the expression from a picture (above) can be viewed as expression on integer or real numbers, vectors, matrix etc.

3.5 Execution Model

3.5.1 Memory

A memory is some area which can contain (data) structures. The quirks architecture distinguishes several types of memory. These memory types reflects programming paradigm which are used in the most programming languages.

1. Static (‘st’). It is a memory which stores global data or data of a module.
2. Dynamic (‘dn’). It is a memory which stores dynamically allocated structures. Can be allocated in a procedure. The UVM provides some control of the dynamic memory usage but not provides any mechanisms like garbage collector.
3. Constant (‘ct’). It contains all constants which a program can use. It is analogue of immediate operands. When generate native code it is transformed to an immediate operand.
4. Local for a procedure (‘lv’). It contains all local variables.
5. Parameter frame (‘fp’). It contains parameters which a caller transmits to a callee and all cells which will contain the call results. ‘fp’ is a referenced memory (see the next point).
6. Pseudo memory (‘dx’, ‘dy’). It is referenced memory, i.e., the ‘dx’ and ‘dy’ cells can’t contain any value but points to a values in other cells. But it is transparent to a programmer and he or she can use the same instructions as for access to a not referenced memory.
7. Arithmetic memory (‘au’). It represents input/output cells of arithmetic modules.

3.5.2 Selectors

Any memory access can be performed only through a selector. A selector is a register which unambiguously defines type of a memory, address and used descriptor. The selector to descriptor binding frequently is performed in runtime and it allows system of dynamic typing to be used. A number of selectors which uses one type of memory is, in a general case, unlimited. An access to selector elements is performed by order (static rules) or by index (dynamic rules for access to regular structures).

3.5.3 Environment

An environment is some external program which loads UVM executable modules, forms memory areas (‘st’, ‘ct’, ‘fp’), prepares input data and starts procedures.

The execution module structure is described in ___. Each module contains one or several procedures, the symbol table with procedure names and entry points. After loading a linking process can be started. This process is described in ___. After linking the environment forms memory areas which are demanded and sets start data. Then the environment runs procedures. The result of working is red from this memory areas. Then the environment uses the results. The procedures can’t change anything besides this memory (‘st’ and ‘fp’).

3.5.4 The model of a procedure

A procedure is a code fragment which has several properties. This features can be divided into 2 groups - static (the feature is the same for all running of this procedure) and dynamic. The static properties are:

• An entry point. It is defined by a module identifier and a procedure name.
• A local memory descriptor (‘lv’, levels 1 - 3).
• A used selectors set (‘dn’, ‘dx’, ‘dy’ - only a set, not descriptors).
• A mapping tables in each point of the procedure.

The dynamic properties are the following:

• An ‘fp’ descriptor (all levels).
• An environment descriptors (‘st’, ‘ct’ - all levels).

An instantiation of a procedure is a fixing of using the procedure. It is an object which fixes all dynamic procedure properties, i.e., in an instantiation all levels of all descriptors are known.

When we instantiate a procedure we have possibility to build a native code also. It is important to be mentioned here: a procedure may have a generic possibilities but an instantiation is fully concrete.

A procedure call looks like as follows:

1. A caller calls the procedure and give some selector to it as a parameter frame.
2. In the calling time the UVM stores all local selectors of the caller and the address of return. The passed frame maps on the new ‘fp’. The ‘lv’ selector is allocated (a static data from instance is used).
3. At the end of the callee code is a return point. The UVM deallocates all local memory and restores selectors of the caller.